Page 14 - Matemáticas para bacharelato de adultos

14
5. Operacións con coordenadas
Prácticas

)
( ) ( )( 1,3− −
+
=
−
I.  (u v− ) + w  u  v  w = − 1 2,1 1 − ) + ( 3 3, 1− =
= ( 2, 1− − ) ( 1,3+ − ) ( 3 3,+ − 3 ) ( 3 3 3,2= − + − ) 3 .
II. (u v − )  + w = − ( 1 3, 2− ) + ( 3 3, 1− ) ( 3,2= − ) ( 3 3,+ − ) 3 = ( 3 3 3,2− + − ) 3 .
9.3. De dúas maneiras:
1 2
)
−

I.  (u + 2w ) − v =  u + 2 w  = (2,1 + (3, 1− ) ( )( 1,3− − 1 − ) =
v
3 3
+
 2 1   2   2 6 3 1 2 9   5 8 
−
−
+
+
=
=  ,   2,−  + ( 1,3− ) =  ,   ,  .
 3 3   3   3 3   3 3 
1  8 1   5 8 
) 
II.  (u + 2w − v = (8, 1− ) ( )( 1,3− − 1 − ) =  ,−  + ( 1,3− ) =  ,  .
3  3 3   3 3 
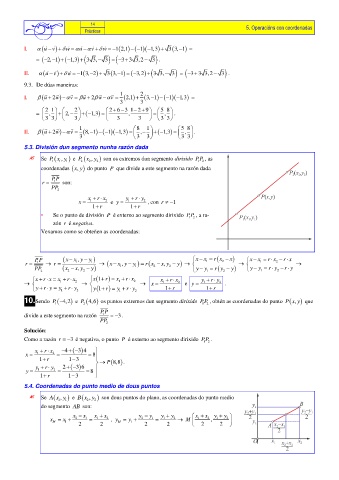
5.3. División dun segmento nunha razón dada
 P , x y P x , y ) son os extremos dun segmento dirixido PP , as
1
2
Se ( 1 1 ) e ( 2 2 1 2
)
coordenadas ( ,x y do punto P que divide a este segmento na razón dada
PP
r = 1 son:
PP 2
x + r x y + r y


x = 1 2 e y = 1 2 , con r  − 1
+
+
1 r 1 r
• Se o punto de división P é externo ao segmento dirixido PP , a ra-
1 2
zón r é negativa.
Vexamos como se obteñen as coordenadas:

−


−

PP (x x y y− , − )  x x = ( r x − ) x  x x = r x − r x
r = 1 → r = 1 1 → (x x y y− , − ) r x= − , x y − ) y →  1 2 →  1 2 →


−
PP 2 (x − 2 , x y − 2 ) y 1 1 ( 2 2   y y = ( r y − ) y  y − y = r y − r y
2
1
1
2



+
 x r x = x + r x  x (1 r+ ) = x + r x x + r x y + r y



→  1 2 →  1 2 → x = 1 2 e y = 1 2 .
+


+
+

 y r y = y + r y 2   y (1 r+ ) = y + r y 2 1 r 1 r
1
1
)
10. Sendo ( 4,2P − ) e (4,6P ) os puntos extremos dun segmento dirixido PP , obtén as coordenadas do punto ( ,P x y que
1 2 1 2
PP
divide a este segmento na razón 1 = − 3.
PP
2
Solución:
Como a razón r = − 3 é negativa, o punto P é externo ao segmento dirixido PP .
1 2

x + r x − 4 + ( ) 3 4− 
x = 1 2 = = 8 
−
+
1 r 1 3  → P (8,8 .
)

y + r y 2 + ( ) 3 6− 

y = 1 2 = = 8
+

−
1 r 1 3 
5.4. Coordenadas do punto medio de dous puntos
 A , x y B x , y ) son dous puntos do plano, as coordenadas do punto medio
Se ( 1
1 ) e ( 2 2
do segmento AB son:
x − x x + x y − y y + y  x + x y + y 2 
x = x + 2 1 = 1 2 , y = y + 2 1 = 1 2 → M  1 2 , 1 
1
M
M
1
2 2 2 2  2 2 