Page 11 - Matemáticas para bacharelato de adultos

11
Vectores no plano. Repaso
Prácticas

4.5. Dependencia e independencia lineal
 Dise que varios vectores son linealmente dependentes se un deles se pode expresar como combinación lineal dos res-
tantes. Cando varios vectores non son linealmente dependentes dise que son linealmente independentes.

TEOREMA 1. Se x , y , …, z son linealmente independentes, a igualdade vectorial (combinación lineal nula):
 x  + + z  = 0
+
y
0
só se satisface para  = ,  = , …,  = (combinación lineal nula trivial).
0
0

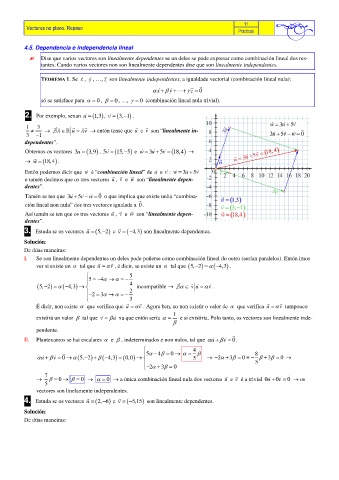
2. Por exemplo, sexan u = ( ), v = (3, 1− ) .
1,3
1  3 →  u = v   → entón tense que u e v son “linealmente in-
3 − 1
dependentes”.
)
)
Obtemos os vectores 3u = (3,9 , 5v = (15, 5− ) e w = 3u + 5v = (18,4 →
)
→ w = (18,4 .
Entón podemos dicir que w é “combinación lineal” de u e v : w = 3u + 5v
e tamén decimos que os tres vectores u , v e w son “linealmente depen-
dentes”.
Tamén se ten que 3u + 5v w = o que implica que existe unha “combina-
−
0
ción lineal non nula” dos tres vectores igualada a 0 .
Así tamén se ten que os tres vectores u , v e w son “linealmente depen-
dentes”.
3. Estuda se os vectores u = (5, 2− ) e v = ( 4,3− ) son linealmente dependentes.
Solución:
De dúas maneiras:
I. Se son linealmente dependentes un deles pode poñerse como combinación lineal do outro (serían paralelos). Entón imos
ver si existe un  tal que u =  v , é dicir, se existe un  tal que (5, 2− ) = ( 4,3− ) .
 5

 5 = − 4 →  = − 4

(5, 2− ) = ( 4,3− ) →  incompatible →  u   = v .
 2 = 3 →  = − 2
 −
  3
É dicir, non existe  que verifica que u =  v . Agora ben, ao non existir o valor de  que verifica u =  v tampouco
1
existirá un valor  tal que v =  u xa que entón sería  = e si existiría. Polo tanto, os vectores son linealmente inde-

pendente.
II. Plantexamos se hai escalares  e  , indeterminados e non nulos, tal que u  + v = 0 .
 4
0

+
 u  = 0 →  (5, 2− ) + ( 4,3− ) (0,0= ) →  5 − 4 = →  = 5  → 2− + 3 =  − 8  + 3 = →
v
0
0
 5
 −

 2 + 3 = 0
7
→  0 →  = = 0 →  = 0 → a única combinación lineal nula dos vectores u e v é a trivial 0u + 0v = 0 → os
5
vectores son linelamente independentes.
4. Estuda se os vectores u = (2, 6− ) e v = ( 5,15− ) son linealmente dependentes.
Solución:
De dúas maneiras: